Quantum Computing (3) – infaktum.de

Im zweiten Teil der Reihe haben wir gesehen, wie durch die Hadamard-Matrix ein Qubit in eine Superposition versetzt wird. Eine Messung diese Qubits liefert nun ein zufälliges Ergebnis. Mehr ist bislang „nicht drin“.

Quantenregister

Wie in der klassischen Computertechnik wird es erst durch die Zusammenfassung mehrerer Qubits möglich, echte Berechnungen anzustellen. In Analogie zu den Registern bei herkömmlichen Rechnern nennen wir diese zusammengehörenden Qubits Quantenregister. Und auch diese sind mit dem im Buch beschriebenen Kalkül kein Problem für uns. Kombinierte Quantensysteme werden durch das Tensorprodukt beschrieben.

Der einfachste Fall ist ein Quantenregister, das aus zwei Qubits zusammengesetzt wird. Mit der Dirac-Notation ist das Rechnen mit diesen zusammengesetzten Systemen recht einfach, und wenn wir die Zustände von Qubits wieder mit $\ket{0}$ und $\ket{1}$ bezeichnen, so können wir die möglichen Zustände eine 2-Qubit-Registers mit $\ket{00}, \ket{01}, \ket{10}$ und $\ket{11}$ bezeichnen. Die Analogie zur bekannten Schreibweise von Zahlen in Binärschreibweise ist offensichtlich; so steht etwa die Binärzahl 10 für die Zahl 2. Wir können mit zwei Qubits also schon bis 4 zählen, bzw. von 0 bis 3. Ein Anfang ist also gemacht. Mit jedem weiteren Qubit verdoppelt sich der Zahlenbereich, genau wie in der klassischen Informatik. Es gibt jedoch einen großen Unterschied: Mit jedem Qubit verdoppelt sich die Dimension des Zustandsraums des Registers.

Die Basisdarstellung

Die Dimension des Tensorproduktraums ergibt sich als Produkt der Dimensionen der einzelnen Zustandsräume. Damit hat der Zustandsraum eine 2-Qubit-Registers die Dimension 4. Die Basisvektoren kennen wir bereits: $\ket{00}, \ket{01}, \ket{10}$ und $\ket{11}$ . Es sind die möglichen Produkte aus den Basisvektoren $\ket{0}$ und $\ket{1}$ des 1-Qubit-Raums. Und wir haben in Teil 1 der Reihe gesehen, wie wir diese Vektoren in Komponentenweise darstellen:

$\ket{0} = \begin{pmatrix} 1\\0\end{pmatrix}, \;\; \ket{1} = \begin{pmatrix} 0\\1\end{pmatrix}.$

Nach den Tensorproduktregeln ergibt sich nun für die Komponenten der Basisvektoren unseres Quantenregisters:

$\ket{00} = \begin{pmatrix} 1\\0\\0\\0\end{pmatrix}, \;\; \ket{01} = \begin{pmatrix} 0\\1\\0\\0\end{pmatrix}, \;\; \ket{10} =\begin{pmatrix} 0\\0\\1\\0\end{pmatrix}, \;\; \ket{11} = \begin{pmatrix} 0\\0\\0\\1\end{pmatrix}.$

Wie man sieht, ist es leicht, aus der Komponentenschreibweise den Wert des Quantenregisters abzulesen, wenn man von oben nach unten schaut und bei 0 beginnt zu zählen. Hat unserer Register n Qubits, so haben wir $2^n$ Basisvektoren, deren Komponenten jeweils $2^n$ Elemente enthalten. Bis auf eine 1 sind alle diese Komponenten 0, und steht diese 1 an der k. Stelle, so handelt es sich um die Zahl $k-1$ .

Operationen auf Quantenregistern

Operationen auf Quantenregistern können durch Matrizen dargestellt werden, die unitär sein müssen. Eine dieser Matrizen ist die Hadamard-Matrix, die wir bereits kennengelernt haben und ein Qubit in eine Superposition versetzt. Wie sieht die Hadamard-Matrix für unser Quantenregister aus? Mit den Regeln für das Tensorprodukt ist die Berechnung einfach:

$H_2 = H \otimes H = \frac{1}{\sqrt{2}}\begin{pmatrix} 1 & 1 \\ 1 & -1\end{pmatrix} \otimes \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1\end{pmatrix}= \frac{1}{2} \begin{pmatrix} 1&1&1&1 \\ 1&-1&1&-1 \\ 1&1&-1&-1 \\ 1&-1&-1&1 \end{pmatrix}.$

CNOT-Gatter

Ein weitere wichtige Operation ist die CNOT-Operation, die bei einem 2-Bit-Register die beiden letzten Komponenten vertauscht:

$\text{CNOT} = \begin{pmatrix} 1&0&0&0 \\ 0&1&0&0 \\ 0&0&0&1 \\ 0&0&1&0 \end{pmatrix}.$

Was fängt man mit dieser Matrix an? Offenbar wirkt sie wie folgt auf unsere Basiszustände:

$\ket{00} \rightarrow \ket{00}, \ket{01} \rightarrow \ket{01},\ket{10} \rightarrow \ket{11}, \ket{11} \rightarrow \ket{10}.$

Das zweite Qubit wird also genau dann „vertauscht“ (d.h. aus 0 wird 1 und umgekehrt), wenn das erste Qubit 1 ist. CNOT wirkt also als Negations-Operator auf dem zweiten Qubit, wenn das erste Quibit auf 1 steht, ansonsten bleibt das zweite Qubit erhalten. Wegen dieser Eigenschaft wird dieser Operator der „Controlled-Not“-Operator genannt, oder kurz CNOT-Gatter. Auch das Wort Gatter stammt aus der klassischen Informatik.

Im Gegensatz zur Hadamard-Matrix brauchten wir bei dieser Matrix keinen Skalierungsfaktor vor der Matrix, damit die Matrix unitär ist. Jede Matrix, die in jeder Zeile und jeder Spalte genau eine 1 und ansonsten nur Nullen hat, ist unitär. Sie werden Permutationsmatrizen genannt, da sie genau die Operationen sind, die die Basisvektoren vertauschen.

Das CNOT-Gatter wird in unserer grafischen Darstellung so präsentiert:

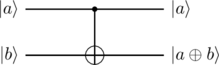
Verschränkung zweier Qubits

Mit dem CNOT-Gatter wird eine Operation definiert, die auf zwei Qubits wirkt. Dabei wird das zweite Qubit negiert, wenn das erste Qubit den Wert 1 hat, ansonsten bleibt es unverändert. Daher der Name „Controlled NOT“. Der Wert des zweiten Qubits ist damit vom ersten Qubit abhängig. Solange der Wert des ersten Qubits bekannt ist, kennen wir auch den Wert des zweiten. Wenn wir das erste Qubit in einer Superposition bringen, so gilt die Unbestimmtheit des ersten Qubits auch für das zweite. Und mehr noch: Die beiden Qubits sind nun verschränkt!

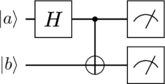
Das obere Qubit wird durch den Hadamard-Operator in eine Superposition versetzt. Eine Messung (die wir hier durch den Kasten mit der stilisierten Skala symbolisieren) am rechten Ende liefert mit 50%iger Wahrscheinlichkeit den Wert 0 oder den Wert 1. Dasselbe gilt durch die Verknüpfung mit dem CNOT-Gatter für das untere Qubit. Aber: Messen wir das obere Qubit, so kennen wir auch den Wert des unteren Qubits, ohne es messen zu müssen. (Dasselbe gilt auch bei einer Messung des unteren Qubits.) Das ist genau das Wesen der Verschränkung. Das Unverständliche / Unheimliche / Unglaubliche dabei: Die Verschränkung durch das CNOT-Gatter findet ja vor der Messung statt! Trotzdem ist nach der Messung des einen Qubits auch der Wert des anderen festgelegt.

Die Messung, die am rechten Ende stattfindet und die wir durch den Kasten mit einer stilisierten Skala darstellen, ist natürlich kein unitärer Operator! Die Messung zerstört ja die Superposition der Qubits, sie beendet den quantenmechanischen Rechenprozess und liefert die für uns relevanten Ergebnisse. Sie erzeugt völlig zufällige Ergebnisse, im Gegensatz zum Determinismus der klassischen Physik und damit auch der klassischen Computertechnik.

Zusammenfassung

Langsam nehmen wir Fahrt auf. Mit den Quantenregistern haben wir im wahrsten Sinne des Wortes neue Dimensionen erreicht, und mit CNOT unser erstes „echtes“ Rechengatter kennengelernt. Und vor allem haben wir die erste Verschränkung von Qubits erlebt. Im nächsten Teil lernen wir den ersten echten Quanten-Algorithmus der Geschichte kennen.