Quantum Computing (2) – infaktum.de

[„Love & Mathematics“ by Lost Archetype is licensed under CC BY-NC-ND 2.0.]

Superposition

Im ersten Teil zu Quantum Computing haben wir gesehen, wie wir mit Hilfe der Pauli-Matrix $P_x$ ein Qubit invertieren können. Wir habe dies grafisch so beschrieben:

Alle Operationen auf Qubits müssen entsprechend den Gesetzen der Quantenmechanik durch unitäre Operatoren erzeugt werden. Und die drei Pauli-Matrizen $P_x,P_y,P_z$ sind unitär.

Eine weitere wichtige Matrix beim Quantum Computing ist die Hadamard-Matrix:

$\text{H} = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1\\1 &-1\end{pmatrix}.$

Sie wirkt so auf unsere Basisvektoren $\ket{0}$ und $\ket{1}$ :

$\begin{split}\text{H} \ket{0} & = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1\\1 &-1\end{pmatrix} \begin{pmatrix} 1 \\ 0\end{pmatrix} = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ 1\end{pmatrix} = \frac{1}{\sqrt{2}} (\ket{0} + \ket{1})\\\text{H} \ket{1} & = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1\\1 &-1\end{pmatrix} \begin{pmatrix} 0 \\ 1\end{pmatrix} = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ -1\end{pmatrix} = \frac{1}{\sqrt{2}} (\ket{0} -\ket{1}).\end{split}$

Die Hadamard-Matrix versetzt die beiden Basisvektoren in eine Superposition.

Willkommen im Quantencomputer!

Was passiert mit dem Qubit im Zustand $\ket{0}$ , nachdem die Hadamard-Matrix darauf operiert hat? Hier ein paar Antworten zur Auswahl:

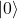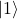Das Qubit befindet sich in beiden Zuständen $\ket{0}$ und $\ket{1}$ gleichzeitig.
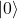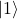Das Qubit befindet sich in allen Zuständen zwischen $\ket{0}$ und $\ket{1}$ gleichzeitig.
Das Qubit befindet sich in keinem definierten Zustand.
Das Qubit ist kaputt.
Wir wissen es nicht.

Keine dieser Antworten ist richtig, und immer noch von unserer klassischen Sicht auf die Dinge bestimmt. Richtig ist: Das Qubit befindet sich in einer Superposition der beiden Zustände. Diese Superposition entzieht sich unserer Anschauung, aber wir haben die mathematischen Werkzeuge, um sie zu beschreiben.
An dieser Stelle passt Richard Feynmans berühmtes Zitat: „Ich denke, man kann mit Sicherheit sagen, dass niemand die Quantenmechanik versteht„. Aber wir müssen die Quantenmechanik nicht verstehen, wenn wir damit rechnen wollen.

Die Messung

Was fangen wir nun mit diesem Qubit an? Es scheint ja nicht mehr Teil unserer realen und logischen Welt zu sein. Um seinen Zustand zu erfahren, müssen wir es irgendwie in die reale Welt zurückholen. Wie wir wissen, geht das mit einer Messung seines Zustands. Beim Spin könnten wir etwa die $z$ -Komponente messen und erhalten dann entweder up oder down. Bei der Messung wird der überlagerte Zustand des Systems zerstört, und das Qubit nimmt wieder den Zustand $\ket{0}$ oder $\ket{1}$ an. Wenn wir gehofft haben, das Qubit könnte gleichzeitig alle Wert zwischen 0 und 1 speichern, so werden wir enttäuscht. Vielleicht war das wirklich so, aber um einen Wert auszulesen, müssen wir eine Messung vornehmen, und dann sind wieder nur die Werte 0 oder 1 möglich. In einem Qubit lässt sich also nur ein Bit an Information speichern. Es wäre so schön gewesen, aber wir hätten das „Minus-Erste Gesetz“ verletzt.

Aus den Vorlesungen wissen wir, dass die Messung keine unitäre Operation ist. Sie zerstört die zeitliche Entwicklung, die durch die Schrödingergleichung definiert und deterministisch ist. Das Quantensystem nimmt dabei zufällig einen der möglichen Zustände an, und wir können lediglich aus der Art der Superposition berechnen, wie die Wahrscheinlichkeitsverteilung für die einzelnen Ergebnisse ist. Im Fall des Qubits sind die möglichen Werte 0 und 1, und nach der Hadamard-Operation beträgt die Wahrscheinlichkeit für beide Werte $\frac{1}{2}$ .

Ein teurer Münzwurf

Was können wir mit dem bisher erreichten anfangen? Wir haben die Hadamard-Matrix, die ein Qubit in eine Superposition überführt, und wir können danach den Wert des Qubits messen. Grafisch können wir das so darstellen:

Der Kasten $H$ steht für die Hadamard-Operation, und der Kasten $M$ steht für die Messung. Der Ausgang ist völlig unbestimmt; $\ket{?}$ nimmt mit gleicher Wahrscheinlichkeit den Wert 0 oder 1 an.

Wir haben mit unserem kleinen Schaltkreis also das Gegenstück zu einer Münze entwickelt. Ziemlich viel Aufwand, um zufällig Kopf oder Zahl zu werfen. Aber vergessen wir eins nicht: Die klassische Mechanik geht davon aus, dass es keinen Zufall gibt. Ein Münzwurf erscheint uns nur deswegen als Sinnbild für den Zufall, da wir nicht alle Parameter kennen, die die Münze beeinflussen. Und das sind in letzter Konsequenz alle Atome des Universums.

Mit diese „Quantenmünze“ haben wir aber einen echten Zufallszahlengenerator. Die Quantenemechanik sagt, dass dies die perfekte Münze ist, und dass wir eine völlig zufällige Reihe von Nullen und Einsen erzeugen. Das ist mit keinem klassischen Computer möglich.

Es stellt sich die Frage: Wie wollen wir mit einem Computer rechnen, bei dem beim Auslesen der Ergebnisse der Zufall regiert?

Zusammenfassung

Wir haben eine der wichtigsten Operationen auf Qubits kennengelernt: Die Hadamard-Matrix, mit der wir Qubits in Superposition bringen können. Um Qubits auszulesen, müssen wir sie messen, und die Superposition wird zerstört. Das Ergebnis der Messung unterliegt zwar gewissen Gesetzen, ist aber völlig zufällig.