Overfitting – infaktum.de

Das Vorgehen der linearen Regression lässt sich verallgemeinern auf Polynome $n.$ Grades der Form

$P(x) = a_0 + a_1 x + a_2 x^ 2 + \ldots + a_n x^n.$

Man erhält dann ein System aus $n+1$ linearen Gleichungen für die Parameter $a_0, a_1,\ldots,a_n$ , wobei die Koeffizienten aus den Wertepaaren $x_k,y_k$ berechnet werden. Die Lösung des Gleichungssystems ist aufwändig aber unkompliziert. Für große $n$ wächst der Aufwand aber stark an. Allerdings sind wir i.d.R. nicht an Polynomen 100. Grades interessiert, sondern eben an einfachen Lösungen, neben linearen also an Polynomen etwa 2. oder 3. Grades.

Grundsätzlich lässt sich zu $N$ Wertepaaren ein Polynom vom Grad $N-1$ findet, das genau durch alle Punkte geht. Dies ist aber nicht das, was wir suchen, denn wir ersetzen dann $N$ Wertepaare lediglich durch $N$ Koeffizienten.

Versuchen wir das einmal an einem Beispiel aus der Linearen Regression. mit den drei Wertepaaren $(1,5),(3,10),(6,13).$

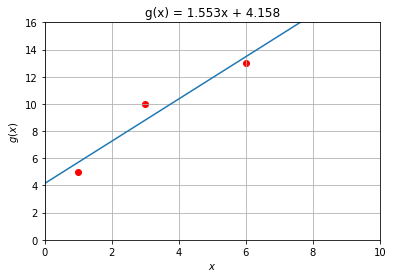
Wir erhalten als Ergebnis der Linearen Regression nebenstehende Gerade. Keiner der drei Punkte liegt auf der Geraden, aber die Fehlerquadratssumme ist die kleinste unter allen anderen linearen Funktionen. Versuchen wir es einmal mit einer Funktion 2. Grades.

Approximation durch ein Polynom 2. Grades

Wir haben die Berechnung bei der Polynomialen Regression bereits beschrieben und wenden die Funktionen hier auf unsere Beispiele an

x,y = np.array([1,3,6]),np.array([5,10,13])

a = poly_reg(x,y,2)
P = poly_gen(a)

x1 = np.linspace(0,6,20)
y1 = [P(xk) for xk in x1 ]

plt.figure( figsize=(6, 4))
poly_plot(x,y,a)
plt.show()

Abb. 1: Wie erwartet geht die Parabel genau durch alle drei Punkte.

Und so geht ein Polynom 6. Grades durch die Punkte:

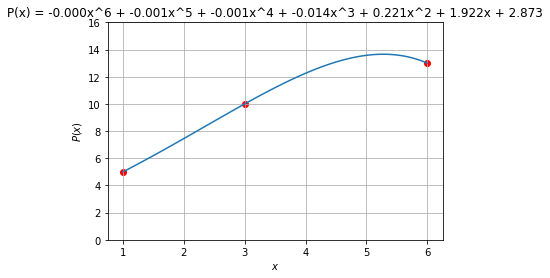
Abb. 2: Das sieht schon etwas krumm aus. Dies ist sicher nicht der wahre Zusammenhang zwischen den drei Punkten.

Overfitting – Zuviel des Guten

Mt höhergradigen Polynomen lässt sich die Differenzfunktion immer weiter verkleinern. Dies ist aber nicht immer wünschenswert, denn mit jeder Erhöhung des Grads des Polynoms entsteht ein neuer Parameter. Dabei entstehen kleine Abweichungen oft nur durch Messfehler bei der Datenerhebung. In der regel ist ein Polynom niedrigen Grades gewünscht, ideal ist eine Ausgleichsgrade.

Diese Überanpassung ist ein bekanntes Problem der Ausgleichsrechnung und wird oft auch Overfitting genannt. Es liegt am Anwender der Algorithmen, solches Overfitting zu vermeiden. Wir demonstrieren hier Overfitting durch hochgradige Polynome an verrauschten Daten, die eigentlich auf einer quadratischen Parabel liegen.

N = 50
x = np.linspace(-3,3,N)
y = np.array([ (value-N/2)**2 for value in range(N)]) + 15*np.random.normal(0,3,N)


fig = plt.figure( figsize=(10, 8), dpi=80)

ax = fig.add_subplot(1,1,1)
ax.set_xlabel('x')
ax.set_ylabel('P(t)')
ax.grid()
ax.set_title("Ausgleichs-Polynome")

print(np.polyfit(x,y,2)[::-1])
P = poly_gen(np.polyfit(x,y,2)[::-1]) 
ax.plot(x,[P(x) for x in x])

#ax.plot(x,y(x,w),label='Original',zorder=0)
for n in (2,10,20):
    P = poly_gen(np.polyfit(x,y,n)[::-1])
    xs = np.linspace(-3,3,200)    
    ax.plot(xs,[P(x) for x in xs],label=f'Regression {n}. Ordnung, D = {D(x,y,P):0.2f}',zorder=0)
ax.scatter(x,y,color='red',marker='o',s = [2 for n in range(len(x))])
ax.legend()
plt.show()

Abb. 3: Verschieden Ausgleichspolynome für dieselben Messdaten

Die Polynome höherer Ordnung versuchen durch starke Krümmungen, möglichst vielen Punkten nahezukommen. Sie geben sicher nicht den korrekten Zusammenhang zwischen den Punkten wieder.