Lineare Regression – infaktum.de

Das Problem

Wir haben eine Reihe von Messpunkten $(x_1,y_1),\ldots,(x_N,y_N)$ .

Um uns einen Überblick zu verschaffen, zeichnen wir sie in einem Diagramm auf, und sie scheinen längs einer Geraden zu liegen, wenn auch nicht exakt. Wir vermuten einen linearen Zusammenhang, d.h. dass die Messwerte durch eine einfache Funktion dargestellt werden kann, und dass Abweichungen durch Messfehler hervorgerufen wurden.

Wir suchen nun eine lineare Funktion $g$ , so dass für alle $k$ gilt: $g(x_k) \approx y_k$ , und dies in einer noch zu definierenden optimalen Weise. Mit einer linearen Funktion meinen wir dabei, dass $g$ von der Gestalt $g(x) = m x + b$ ist mit zwei Zahlen $m$ und $b$ . Diese Gleichung haben wir in der Schule als Geradengleichung kennengelernt. (Mathematisch korrekt spricht man von einer affinen Funktion, denn für lineare Funktionen gilt $g(0) = 0$ . Darauf kommen wir noch zurück).

Im Allgemeinen wird $g$ nicht durch alle gegebenen Punkte gehen, wenn diese nicht wirklich auf einer Linie aufgereiht sind.

Der einfachste Fall: 2 Punkte

Wenn wir nur zwei Punkte $(x_1,y_1)$ und $(x_2,y_2)$ haben, so finden wir natürlich eine Gerade durch diese Punkte. Die Rechnung ist einfach: Wir berechnen $m$ durch

$m = \frac{y_2 - y_1}{x_2 - x_1}$

und erhalten so die Steigung $m$ der Geraden $g$ .

Den Wert für $b$ erhalten wir dann durch Einsetzen von $m$ in die Gleichung $g(x_1) = m x_1 + b = \frac{y_2 - y_1}{x_2 - x_1} x_1 + b = y_1$ , also

$b = y_1 - \frac{y_2 - y_1}{x_2 - x_1} x_1 = y_1 - m x_1$

Implementierung in Python

Mit Hilfe von NumPy können wir die Berechnung der Geraden $g$ „direkt hinschreiben“.

import numpy as np
import matplotlib.pyplot as plt

def g(x,y):
    '''Berechnet die Gerade durch zwei Punkte'''
    m = (y[1] - y[0]) / (x[1] - x[0])
    b = y[0] - m * x[0] 
    return lambda x: m * x + b

# Test für zwei Punkte

xp = [1,5]
yp = [3,8]
x = np.arange(0,8)
    
plt.ylim(0,10)
plt.xlab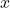el('')
plt.ylabel('')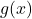
plt.scatter(xp,yp)
plt.plot(x,g(xp,yp)(x))

plt.show()

Abb. 2: Durch zwei Punkte geht immer genau eine Gerade

Die Lineare Regression

Was macht man nun bei mehr als zwei Punkten, die nicht exakt auf einer Geraden liegen? Wie finden wir eine Ausgleichsgerade, die „möglichst nahe“ an allen diesen Punkten liegt? Dann könnten wir die Gerade als Funktion betrachten, die diese Wertepaare erzeugt, wobei die Abweichungen möglichst klein sind. Dabei wird es eher die Regel sein, dass die Gerade nicht einmal durch einen einzigen dieser Punkte läuft. Ausgehend von dieser Gerade könnten wir dann Werte zwischen den gegebenen Punkten vorhersagen (interpolieren), oder die Werte von Punkten, die links oder rechts von unserem Messbereich liegen (extrapolieren).

Dazu müssen wir erst einmal überlegen, was es bedeutet, dass die Gerade möglichst nahe an allen Punkten liegt und in diesem Sinne optimal ist. Der folgende Ansatz hat sich bewährt:

Zu einer gegebenen Funktion $F$ definiert man den Abstand $D$ der Wertepaare zu dieser Funktion als

$D := \sum_{k=1}^N (F(x_k) - y_k)^2.$

Es wird also summiert über die Quadrate der Differenzen der Funktionswerte und der tatsächlichen Werte.
Warum macht diese Funktion Sinn? Sie bestimmt zu jedem Wertepaar das Quadrat der Abweichung $f(x_k) - y_k$ . Dieses Quadrat ist positiv, und dadurch können sich negative und positive Abweichungen nicht aufheben. Zudem werden größere Abweichung stärker gewichtet. Wir bilden die Summe über alle gegebenen Punkte, dadurch werden alle Wertepaare gleich berücksichtigt. Diese Fehlerquadratsumme ist ein geeignetes Maß, um Funktionen zu bewerten. Dabei spielt es keine Rolle, ob die Funktion ein Polynom ist oder irgendeine andere Form hat.

Gesucht ist nun eine Funktion $F$ , die diese Fehlerquadratsumme minimiert. Bei der Linearen Regression wird dabei eine lineare Funktion gesucht, d.h. eine Funktion der Gestalt

$F(x) = mx + b.$

Der Ansatz wird die Methode der kleinsten Quadrate genannt.

Wie wir gesehen haben, gibt es bei zwei Wertepaaren ( $N=2$ ) genau eine lineare Funktion, die durch die beiden Punkte geht und die $D$ damit zu 0 macht. Für $N>2$ wird es im allgemeinen keine Gerade geben, die durch alle Punkte geht, aber es gibt genau eine Funktion $F$ , die $D$ minimiert. Dies sieht man wie folgt:

Für Funktionen $F(x) = mx + b$ ist die Fehlerquadratsumme

$D(F) = D(m,b) = \sum_{k=1}^N (F(x_k) - y_k)^2 = \sum_{k=1}^N (mx_k + b - y_k)^2$

eine Funktion der beiden Parameter $m$ und $b$ . Gesucht sind zwei Zahlen $m,b$ , so dass $D(m,b)$ minimal ist. Dort muss

$\nabla D(m,b) = 0$

sein, also

$\frac{\partial D}{\partial m} (m,b) = 0, \frac{\partial D}{\partial b} (m,b)= 0$

Dies führt zu dem linearen Gleichungssystem (oder besser dem affinen Gleichungssystem)

(1) $\begin{equation*}\begin{split}\frac{\partial D}{\partial m} (m,b) &= \sum_{k=1}^N 2 x_k(mx_k + b - y_k) = 0 \\\frac{\partial D}{\partial m} (m,b) &= \sum_{k=1}^N 2 (mx_k + b - y_k) = 0\end{split}\end{equation*}$

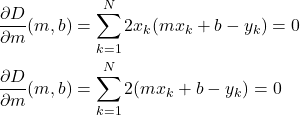
und nach einigen Umformungen (und Streichen der 2)

(2) $\begin{equation*}\begin{split}(\sum_{k=1}^N x_k^2) m + (\sum_{k=1}^N x_k)b &= \sum_{k=1}^N x_k y_k \(\sum_{k=1}^N x_k) m + N b &= \sum_k^N y_k\end{split}\end{equation*}$

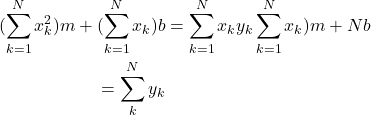
Dieses Gleichungssystem hat die Form

(3) $\begin{equation*}\begin{split}a_1m +b_1 b &= c_1 \\a_2m +b_2 b &= c_2\end{split}\end{equation*}$

und besitzt die eindeutige Lösung

(4) $\begin{equation*}\begin{split}b &= \frac{a_2 c_1 - a_1 c_2}{a_2 b_1 - a_1 b_2}, \\m &= \frac{c_1 - b_1 b}{a_1}. \end{split}\end{equation*}$

Dieses Verfahren lässt sich leicht implementieren. Dazu berechnet man zunächst aus den gegebenen Wertepaaren

$a_1 = \sum x_k^2, b_1 = \sum x_k, c_1 = \sum x_k y_k, \;a_2 = \sum x_k, b_2 = N, c_2= \sum y_k$

und bestimmt dann $m$ und $b$ gemäß der angegebenen Gleichung.

Implementierung der linearen Regression

Wieder können wir mit Hilfe von NumPy die Formeln direkt abschreiben.

def koeff(x,y):
    """
Berechnung der Koeffizienten des Gleichungssystems
    a1*m + b1*b = c1
    a2*m + b2*b = c2
    """
    sum_x = np.sum(x)
    sum_y = np.sum(y)
    sum_xx = np.sum(x * x)
    sum_xy = np.sum(x * y)
    N = x.shape[0]
    return sum_xx, sum_x, sum_xy, sum_x, N, sum_y

def lin_reg(x,y):
    """Einfache Implementierung der linearen Regression"""
    a1, b1, c1, a2, b2, c2 = koeff(x,y)
    # Lösung des Gleichungssystems
    b = (a2 * c1 - a1 * c2) / (a2 * b1 - a1 * b2)
    m = (c1 - b1 * b) / a1
    return (m,b)

def D(x,y,,f):
    """Die Distanzfunktion berechnet die Fehlerquadratsumme"""
    return np.sum((f(x) - y)**2)

Wir implementieren noch einige Hilfsfunktionen für Polynome

def poly_gen(a:np.ndarray):
    """Erzeugt ein Polynom mit den Koefizienten aus a."""
    return (lambda x: np.sum([a[k] * x**k for k in range(a.shape[0])]))

def poly_text(cff):
    """Ausgabe des Polynoms in Text-Form. """
    comp = []
    text = "g(x) = "
    for n,a in enumerate(cff):   
        c = "{:.3f}".format(a)
        if n > 0:
            c += "x"
        if n > 1:
            c += "^" + str(n)
        comp.append(c)

    comp.reverse()
    for c in comp:
        text += c + " + "
    text = text[:-3]
    return text

def poly_plot(x,y,a):
    plt.xlim(0,10)
    plt.ylim(min(0,np.min(y) - 3),np.max(y)+3)
    plt.xlab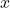el('')
    plt.ylabel('')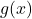
    plt.title(poly_text(a))
    plt.grid(True)
    plt.scatter(x,y,color='red')
    P = poly_gen(a)
    xp = np.linspace(-1,np.max(x)+2,100)
    yp = [P(x) for x in xp]
    plt.plot(xp,yp)

Wir zeigen die Berechnung des Gradienten am (einfachsten) Beispiel mit drei Punkten

x,y = np.array([1,3,6]),np.array([5,10,13])
plt.scatter(x,y,color='red')
plt.show()
g = np.flip(np.array(lin_reg(x,y)))
poly_plot(x,y,g)
plt.show()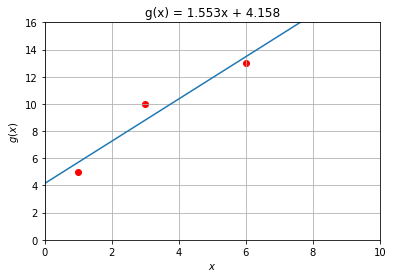

Abb. 3: Die Ausgleichsgerade trifft keinen der drei Punkte

Ein etwas größeres Beispiel

Wir berechnen einige Punkte für die Funktion $F(x) = 3x + 5$ und „verrauschen“ die Messergebnisse. Unsere Ausgleichgerade $g$ sollte dann ähnliche Koeffizienten wie $F$ haben.

N=20
x = np.linspace(1,10,N) + np.random.normal(0,1,N)
y = 3 * x + 5 + np.random.normal(0,3,N)

g = np.flip(np.array(lin_reg(x,y)))

poly_plot(x,y,g)
plt.show()

Abb. 4: Die Ausgleichgerade hat in etwa dieselben Parameter wie die ursprüngliche Funktion

Zur Geschichte des Verfahrens

Das Verfahren wurde Anfang des 19. Jahrhundert von Carl Friedrich Gauß entwickelt. Die wissenschaftliche Welt stand damals vor der Herausforderung, dass der gerade entdeckte Planetoid Ceres hinter der Sonne verschwand, und nun anhand weniger Messdaten wiedergefunden werden musste. Gauß konnte mit seiner neuen Methode die Bahn so gut vorausberechnen, dass die Astronomen wussten, wo sie zu suchen hatten und Ceres sehr schnell wiederentdeckt werden konnte. (s. Methode der kleinsten Quadrate bei Wikipedia.)