Lineare Algebra – infaktum.de

[Abb.: „Linear Algebra“ by brnzwngs is licensed under CC BY-NC-SA 2.0.]

Eine Reihe von Klassikern der Fachliteratur zur Programmierung tragen den Namen Algorithmen und Datenstrukturen. Die Autoren geben Datenstrukturen dieselbe Bedeutung wie den Algorithmen, an die man zuerst bei Programmierung denkt. In der Welt der Mathematik stellen (Daten-)Strukturen die Grundlage dar, auf der alles aufgebaut wird. Die Datenstrukturen, die bei den KNN verwendet wird, stammen aus dem Bereich der Linearen Algebra, der wohl (und glücklicherweise) einfachsten Disziplin der Höheren Mathematik. Wir beschreiben auf dieser Seite die wichtigsten Begriffe aus diesem Teil der Mathematik.

Auch wenn man nicht tief in die für viele mystisch/mysteriöse Welt eintauchen möchte, so sind vor allem die kompakte und einheitliche Schreibweise und die eindeutigen Begriffsbildungen für das Verständnis nicht nur Künstlicher Neuronaler Netze hilfreich. Der praktische Umgang mit diesen Strukturen und den Operationen darauf sind der Schlüssel zum Deep Learning.

Skalare und Vektoren

Ein Skalar ist in der Linearen Algebra einfach eine reelle Zahl, und man verwendet den Begriff nur, um eine skalare Größe von einem Vektor zu unterscheiden. Mit Skalaren zu rechnen haben wir in der Grundschule gelernt.

Ein Vektor fasst mehrere Skalare, die in einem Zusammenhang stehen, zu einer Einheit zusammen. Dies kennen wir aus Koordinaten eines Punktes in einer Ebene, dessen x- und y-Koordinate zusammen den Ortsvektor des Punktes bilden.(Auch das haben wir auf der Schule gelernt.) Die einzelnen Zahlen, aus den der Vektor gebildet wird, nennt man die Komponenten des Vektors, und die Anzahl der Komponenten in einem Vektor wird die Dimenson genannt. Um Vektoren von Skalaren zu unterscheiden, zeichnet man oft einen kleinen Pfeil über den Namen des Vektors, also etwa $\vec{v}$ . Spannend ist nun, dass man mit Vektoren teilweise alles machen kann wie mit Skalaren: Man kann sie addieren, subtrahieren und multiplizieren (aber nich dividieren), und es gibt sogar mehrere Möglichkeiten der Multiplikation.

Wir haben bereits eine andere Sorte von Vektoren kennengelernt, an die man nicht sofort denkt: Auch Polynome können als Vektoren aufgefasst werden! Denn jedes Polynom

$P = a_0 + a_1 x + a_2 x^2 + \ldots + a_N x^N$

ist durch seine Koeffizienten $a_k$ bestimmt, und wir können diese Koeffizienten als Vektor zusammenfassen. Somit ist unser Polynom $P$ ein Vektor der Form

$P=\begin{pmatrix} a_0 \ a_1 \ \dots \ a_N \end{pmatrix}.$

Rechnen mit Vektoren

Wir zeigen an den Beispielen der Ortsvektoren und Polynomen, wie man mit Vektoren rechnen kann.

Die Addition

Zwei Ortsvektoren $\vec{v} = \begin{pmatrix} v_1 \ v_2 \end{pmatrix}$ und $\vec{w} = \begin{pmatrix} w_1 \ w_2 \end{pmatrix}$ werden addiert, indem man einfach die Komponenten addiert: $\vec{v} + \vec{w} = \begin{pmatrix} v_1 + w_1 \ v_2 + w_2\end{pmatrix}$ .

Für Polynome sieht dies so aus:

(1) $\begin{equation*}\begin{split}P(x) + Q(x) &= (a_0 + a_1x+ a_2 x^2 + \ldots + a_N x^N) + (b_0 + b_1x+ b_2 x^2 + \ldots + b_N x^N) \\&= (a_0 + b_0) + (a_1 + b_1)x+ (a_2 + b_2) x^2 + \ldots + (a_N + b_N) x^N\end{split}\end{equation*}$

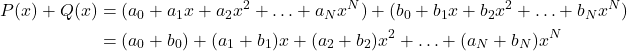
Die Multiplikation mit einem Skalar

Einen Ortsvektor $\vec{v} = \begin{pmatrix} v_1 \ v_2 \end{pmatrix}$ kann man mit einer Zahl $k$ multiplizieren, indem man jede Komponente mit dieser Zahl multipliziert: $k \vec{v} = \begin{pmatrix} k v_1 \ k v_2 \end{pmatrix}$

Und bei Polynomen:

$k P(x) = (k a_0) + (k a_1) x+ (k a_2) x^2 + \ldots + (k a_N) x^N$

Multiplikation zweier Vektoren

Für die Multiplikation zweier Vektoren gibt es mehrere Möglichkeiten, zu denen allerdings die naheliegendste, nämlich einfach die komponetenweise Multiplikation, nicht gehört.

Das Skalarprodukt

Das wichtigste Produkt zweier Vektoren ist das Skalarprodukt, das auch Inneres Produkt oder Punktprodukt (letzteres wegen der Schreibweise) genannt wird:

$\vec{v} \cdot \vec{w} = \begin{pmatrix} v_1 \ v_2 \end{pmatrix} \cdot \begin{pmatrix} w_1 \ v_2 \end{pmatrix}= v_1 w_1 + v_2 w_2$

In höheren Dimensionen lässt sich dies kompakt schreiben als $\vec{v} \cdot \vec{w} = \sum_{k=1}^N v_k w_k$ . Es wird also zwar die komponentenweise Multiplikation durchgeführt, danach werden aber die Ergebnisse aufsummiert, wodurch ein Skalar enteht. Das Skalarprodukt ist von fundamentaler Bedeutung, auch für unsere KNN, so dass wir darüber noch ein eigenes Kapitel schreiben.

Ein zweites Produkt zwischen Vektoren ist das Vektorprodukt oder Kreuzprodukt (wegen der Schreibweise $\vec{v} \times \vec{w}$ ), das allerdings nur für dreidimensionale Vektoren definiert und vor allem für Geometrie und Physik bedeutsam ist. Für unsere Zwecke ist es uninteressant. Das Ergebnis dieses Produkts ist ein Vektor, der senkrecht auf beiden Vektoren steht.

Matrizen

Den nächsten Schritt in unserer Hierarchie stellen Matrizen dar. Eine Matrix ist ein zweidimensionales Zahhlenschema der Gestalt $M = \begin{pmatrix} a_{11} & \ldots a_{1n} \ \ldots \ a_{m1} & \ldots a_{mn} \end{pmatrix}$ . Man spricht hier von einer $m\times n$ -Matrix, und ist $m=n$ , so heißt die Matrix quadratisch.

Sind Vektoren die Datenstrukturen der Linearen Algebra, so sind Matrizen die Operationen darauf. Ein Vektor lässt sich nämlich it einer Matrix multiplizieren, wodurch ein neuer Vektor entsteht (dazu müssen natürlich die Dimensionen „passen“)

$\begin{equation*}\begin{split}M \cdot v &= \begin{pmatrix} a_{11} & \ldots a_{1n} \ \ldots \ a_{m1} & \ldots a_{mn} \end{pmatrix}\begin{pmatrix} v_1 \ \ldots \ v_n \end{pmatrix} \\&=\begin{pmatrix} \sum_{k=1}^n a_{1k} v_k \ \ldots \ \sum_{k=1}^n a_{mk} v_k \end{pmatrix}.\end{split}\end{equation*}$

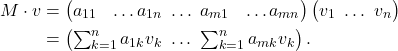
Hinter den vielen Indizes versteckt sich folgendes Rechenschema: Man nimmt die erste Zeile der Matrix und multipliziert die Komponenten mit den Komponenten des Vektors. Die Summe bildet die erste Komponente des Ergebnis-Vektors. Dann geht es mit der zweiten Zeile weiter, bis alle Zeilen der Matrix abgearbeitet sind. Die $k.$ Komponente des Ergebnisvektors ist also das Skalarprodukt der $k.$ Zeile der Matrix mit dem Vektor $\vec{v}$ .

Man kann Matrizen auch addieren (komponentenweise) und sogar multiplizieren, wenn die Dimensionen übereinstimmen. Wir werden bei den KNN auf Matrizen stoßen, wenn wir die Gewichte des Neuronalen Netzes untersuchen.

Tensoren

Natürlich kann man das Spiel weiter treiben und nach den zweidimsionalen Matrizen Zahlenschemata mit noch mehr Dimensionen betrachten. Jenseits der Matrizen spricht man ganz allgemein von Tensoren. Dabei sind Skalare, Vektoren und Matrizen ebenso Tensoren, mit der Dimension 0, 1 bzw. 2. Dabei spricht man bei Tensoren eher von Stufen als von Dimensionen. Jenseits der Matrizen lassen sich Tensoren nicht mehr so schön hinschreiben, aber in Computerprogrammen ist es egal, wie viele Indizes man verwendet. Ein Tensor 3. Stufe ist also eine Menge an Zahlen, die strukturiert in der Form $T = (t_{ijk})$ geschrieben werden können.

Tensoren werden wir in der Einführung zu KNN nicht besprechen. Sie spielen aber in der Programmierung eine wichtige Rolle, und Googles KI-Paket heißt nach diesen Objekten Tensorflow (auch Facebooks Torch basiert auf Tensoren.)

Programmatische Umsetzung

Die vorgestellten Strukturen und Rechenoperationen lassen sich natürlich leicht implementieren. Wir demonstrieren hier einmal die Umsetzung in Python, einmal mit Schleifen, und dann mit dem Paket NumPy. Dabei hat Python gegenüber vielen anderen Sprachen wie Java, C++ und C# einige Vorteile, da es von Natur aus Listen gut unterstützt und etwa im Gegensatz zu Java auch Operator Overloading, was vieles lesbarer macht.

Ohne NumPy

Ohne NumPy stehen unsin Python nur normale Listen zur Verfügung. Das führt normalerweise zu den üblichen (tw. verschachtelten Schleifen), z.B. in Java:

for(int i = 0; i < n; i++){                     
        sum[i] = v[i] + w[i]            
}

In Python lässt sich dies aber eleganter schreiben, da Listen einen großen Stellenwert in dieser Sprache haben.

def summe(v,w):
    return [v+w for v,w in zip(v,w)]

def produkt(k,v):
    return [k * v for v in v]

def skalar_produkt(v,w):
    help = [v*w for v,w in zip(v,w)]
    skalar = 0
    for h in help:
        skalar += h
    return skalar

def produkt_matrix(m,v):
    return [[m*v for m,v in zip(m,v)]  ]

Mit NumPy

Mit NumPy geht alles sehr viel schöner und vor allem schneller, was man erst bei sehr großen Datenmengen merkt. NumPy rechnet intern mit anderen („intelligenten“) Datenstrukturen, daher müssen alle Werte zuerst in ein internes Format umgewandelt werden, das ndarray („N-dimensionales Array“). Danach sind all unsere Operatoren bereits vorhanden. Dank Operator Overloading brauchen wir keine Funktionen zu definieren, und NumPy weiß auf grund der Datenstrukturen zu entscheiden, dass kv das Produkt einer Konstanten mit einem Vektor ist, und Mv das entsprechende Produkt mit einer Matrix.

import numpy as np

k = 3
v = np.array([1,2])
w = np.array([3,4])
m = np.array([[1,2],[3,4]])


print(f'v = {v}, \nw = {w},\nM = {m}\n')

print(f'v + w = {v+w}')
print(f'k v = {k*v}')
print(f'v . w = {v*w}')
print(f'M v = {m * v}')

Dies ergibt die Ausgabe

v = [1 2], 
w = [3 4],
M = [[1 2]
 [3 4]]

v + w = [4 6]
k v = [3 6]
v . w = [3 8]
M v = [[1 4]
 [3 8]]

Mit NumPy werden viele Aufgaben kinderleicht, und der Code ist wirklich leichter zu verstehen.

Aber Achtung: Zu den einzelnen Operatoren gibt es auch andere Implementierung, etwa dot für das Skalarprodukt, die deutlich schneller sind als die Operationen in der „einfachen“ Schreibweise. Wir werden sie auch an passenden Stellen bevorzugt einsetzen.