Mit der Linearen Regression und dem Gradientenabstiegsverfahren haben wir zwei fundamentale Methoden zur Optimierung kennen gelernt. Dabei geht es darum, eine Anzahl Parameter (Gewichte und Bias) so anzupassen, dass eine reellwerte Funktion, die Verlustfunktion L, minimiert wird.
Das Perzeptron ist die erste Implementierung eines Künstlichen Neuronalen Netzes (KNN), obwohl man es heute wegen der einfachen Struktur nicht mehr als solches bezeichnen würde. Es demonstriert aber die Funktionsweise der KNNs.
Aufbau des Perzeptrons
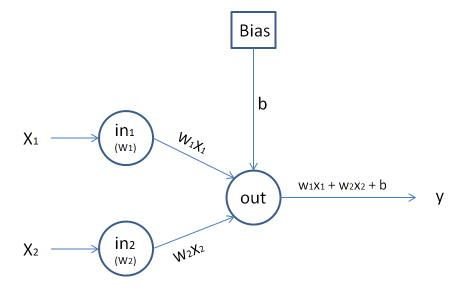
Das einfachste Perzeptron besteht aus zwei Eingabe-Neuronen und einem Ausgabe-Neuron. Die Ein- und Ausgänge verarbeiten nur binäre Daten, d.h. es werden nur 0 und 1 als Ein- und Ausgangssignale verarbeitet.
Als Parameter haben wir zunächst zwei Gewichte ![]() , aus denen die gewichtete Summe
, aus denen die gewichtete Summe ![]() gebildet wird. Liegt diese Summe über einem Schwellenwert
gebildet wird. Liegt diese Summe über einem Schwellenwert ![]() , so liefert der Ausgang den Wert 1, ansonsten die 0. Man sagt auch: Das Neuron feuert, sobald der Schwellenwert überschritten ist:
, so liefert der Ausgang den Wert 1, ansonsten die 0. Man sagt auch: Das Neuron feuert, sobald der Schwellenwert überschritten ist:
Perzeptron-Lernregel
![]()
Statt eines Schwellenwerts wird oft ein Bias ![]() eingeführt und dann mit der Summe
eingeführt und dann mit der Summe ![]() gearbeitet. Ist diese größer 0, so liefert das Perzeptron der Wert 1, ansonsten die 0:
gearbeitet. Ist diese größer 0, so liefert das Perzeptron der Wert 1, ansonsten die 0:
Perzeptron-Lernregel (mit Bias)
![]()
Dieser Bias ist neben den Gewichten der dritte Parameter und gibt den Wert vor, wenn am Eingang nur 0 anliegt.
Das Perzeptron kann als logisches Gatter gedacht werden, mit dem logische Verknüpfungen wie UND und ODER realisiert werden können. Dazu werden die entsprechenden Werte an an die Eingabe-Neuronen ![]() angelegt und der y-Ausgang verarbeitet.
angelegt und der y-Ausgang verarbeitet.
Der Lern-Algorithmus
Beim Training des Perzeptrons werden die Testeingabedaten an die Eingabeneuronen angelegt. Entspricht die Ausgabe dem erwarteten Ergebnis, so bleiben die Gewichte und der Bias unverändert. Bei einem abweichenden Ergebnis werden die Gewichte nach oben bzw. nach unten korrigiert, d.h. es ist
(1) 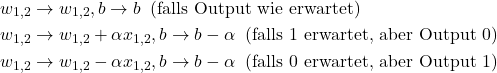
Hierbei sind ![]() die Testdaten und
die Testdaten und ![]() eine Lernrate. Ist
eine Lernrate. Ist ![]() der Output des Perzeptrons, so lässt sich dies vereinfachen zu
der Output des Perzeptrons, so lässt sich dies vereinfachen zu
(2) ![]()
da
Implementierung des Perzeptrons
Tatsächlich ist es mit NumPy wieder sehr einfach, das Perzeptron zu implementieren. Wir formulieren einfach den Lernschritt auf den Gewichten. Dazu definieren wir noch eine „Trainings- und Testfunktion“.
import numpy as np
import matplotlib as plt
def output(x,w,b):
return 1 if np.sum(w * x) + b > 0 else 0
def lernschritt(x,y,w,b,alpha):
o = output(x,w,b)
w += alpha * (y - o) * x
b += alpha * (y - o)
return w,b
def training(testdaten,w, b, alpha=0.01,maxiter=1000):
for i in np.random.randint(4,size=maxiter):
w,b = lernschritt(testdaten[i,0:2], testdaten[i,2],w,b,alpha)
return w, b
# Trainiert und testet ein Perzeptron
def tut(name,daten):
w,b = training(daten,np.zeros(len(daten) - 2),0)
print(f'{name}: ')
print(f'Gewichte= {w}, Bias = {b}\n')
for x in daten:
o = output(x[:-1],w,b)
check = '\u2713' if o == x[2] else '\u21af'
print(f'{x[0]},{x[1]} -> {x[2]}, Output: {o} {check}')
print('\n')Testdaten
Die Testdaten sind recht einfach und stellen die Wahrheitstafeln für UND, NICHT-UND, ODER und XODER dar.
test_und = np.array([[0,0,0],[0,1,0],[1,0,0],[1,1,1]])
test_nund = np.array([[0,0,1],[0,1,1],[1,0,1],[1,1,0]])
test_oder = np.array([[0,0,0],[0,1,1],[1,0,1],[1,1,1]])
test_xoder = np.array([[0,0,0],[0,1,1],[1,0,1],[1,1,0]])
# Und nun wird getestet
tut('UND-Verknüpfung',test_und)
tut('NICHT-UND-Verknüpfung',test_nund)
tut('ODER-Verknüpfung',test_oder)
tut('XODER-Verknüpfung',test_xoder)Wir erhalten als Ergebnis:
UND-Verknüpfung: Gewichte= [0.01 0.01], Bias = -0.01 0,0 -> 0, Output: 0 ✓ 0,1 -> 0, Output: 0 ✓ 1,0 -> 0, Output: 0 ✓ 1,1 -> 1, Output: 1 ✓ NICHT-UND-Verknüpfung: Gewichte= [-0.01 -0.01], Bias = 0.02 0,0 -> 1, Output: 1 ✓ 0,1 -> 1, Output: 1 ✓ 1,0 -> 1, Output: 1 ✓ 1,1 -> 0, Output: 0 ✓ ODER-Verknüpfung: Gewichte= [0.01 0.01], Bias = 0.0 0,0 -> 0, Output: 0 ✓ 0,1 -> 1, Output: 1 ✓ 1,0 -> 1, Output: 1 ✓ 1,1 -> 1, Output: 1 ✓ XODER-Verknüpfung: Gewichte= [0.01 0. ], Bias = 0.01 0,0 -> 0, Output: 1 ↯ 0,1 -> 1, Output: 1 ✓ 1,0 -> 1, Output: 1 ✓ 1,1 -> 0, Output: 1 ↯
Die XODER-Verknüpfung und der erste KI-Winter
Wie man sieht, gibt es bei der XODER-Verknüpfung kein zufriedenstellendes Ergebnis. Eine Analyse zeigt, dass das Perzeptron dieses Aufgabe grundsätzlich nicht lösen kann. Sind etwa bei der UND- und ODER-Verknüpfung die Eingabedaten in der Ebene durch eine Gerade trennbar, so ist dies bei der XODER-Verknüpfung nicht der Fall. Aufgrund der Tatsache, dass ausschließlich lineare Funktionen verwendet werden, scheitert das Perzeptron an dieser scheinbar einfachen Aufgabe.
Tatsächlich führte diese Entdeckung nach der ersten Euphorie zu einem starken Nachlassen des Interesses an der Erforschung künstlicher Intelligenz, was als erster KI-Winter bezeichnet wird.
Die Lösung des XOR-Problems liegt in der Verwendung weiterer Schichten von Neuronen und nicht-linearer Funktionen, und sie führte zur Entwicklung der heute verwendeten Künstlichen Neuronalen Netze.

